Lodret belastet muret væg efter EN 1996 - 1 - 1

Programmodulet "Lodret belastet muret væg" foretager en bæreevneeftervisning efter EN 1996-1-1 af et vægfelt uden åbninger. For en bærende væg med store vinduesåbninger må man derfor beregne hvert vægfelt mellem åbningerne separat. En bærende væg med små vinduesåbninger kan derimod beregnes som en samlet væg. I en væg med store åbninger må den samlede lodrette last på væggen naturligvis fordeles over væggens effektive længde, dvs summen af længderne af de enkelte vægfelter mellem åbningerne.

Modulet bør anvendes, når den lodrette last i det dimensionsgivende tværsnit er større end 15 % af kapaciteten for den aktuelle væg beregnet som en centralt påvirket søjle

Da lasten er en kombination af lodret last, tværlast og excentricitetsmomenter, er bæreevnen ikke blot et enkelt tal. Programmet foretager bæreevneeftervisningen på den måde, at det beregner en formel lodret bæreevne på basis af bl.a. de excentriciteter i væggen, som kommer af den aktuelle lodrette og vandrette last. Den formelle bæreevne afhænger altså af den aktuelle last. Hvis den formelle lodrette bæreevne er større end eller lig med den aktuelle lodrette last, er bæreevnen tilstrækkelig.

I EN 1996 - 1 - 1 tages der hensyn til lastexcentriciteter og søjlevirkning i en væg ved hjælp af en såkaldt kapacitetsreduktionsfaktor Φ idet væggens regningsmæssige bæreevne pr. længdeenhed for lodret last bestemmes som:

• N_Rd = Φ × t × f_d

Her er t væggens tykkelse og f_d er murværkets regningsmæssige trykstyrke. Indeks _R står for resistance som på dansk betyder bæreevne, og indeks _d står for design value som på dansk betyder regningsmæssig værdi.

For at kunne bestemme værdien af kapacitetsreduktionsfaktoren Φ i de 3 snit som EN 1996 - 1 - 1 kræver undersøgt, er det nødvendigt at bestemme den lodrette lasts excentricitet og excentricitetsbidraget fra den vandrette tværlast i de 3 snit.

EN 1996 - 1 - 1 giver i anneks C en metode til bestemmelse af den lodrette lasts excentricitet i toppen og bunden af en væg baseret på en elastisk model af den betragtede væg og de tilstødende vægge og dæk. Denne fremgangsmåde er meget følsom overfor de stivhedsantagelser, der benyttes og i mange tilfælde er resultatet uforeneligt med at der ikke kan regnes med trækspændinger i væggen. Som følge heraf er der i annekset også angivet en metode til bestemmelse af excentriciteterne baseret på en antagelse om, at spændingerne i væggen kan omlejres som følge af revnedannelse således at der ikke optræder trækspændinger. Hvorledes disse metoder kan gøres operationelle fremgår ikke klart.

I programmodulet er valgt en anden fremgangsmåde, der kort fortalt går ud på at undersøge om der i væggen er plads til en trykbue svarende til den lodrette normalkraft og den vandrette last som væggen påvirkes af. I væggens top og bund skal trykbuen ende således, at kraften kan overføres til de tilstødende konstruktioner. Når trykbuens ender er fastlagt er trykbuens placering i midtersnittet bestemt, og kapacitetsreduktionsfaktoren Φ_m og dermed bæreevnen svarende til dette snit kan herefter bestemmes.

Rent inddatamæssigt betyder det, at i stedet for at angive excentriciteten af den lodrette last i væggens top og bund, som man alligevel ikke kan bestemme med nogen grad af sikkerhed, skal man angive et interval i væggens top og bund inden for hvilket trykbuens ender skal befinde sig. Disse intervaller kaldes excentricitetsintervaller.

I midtersnittet er excentriciteten fra lasterne på væggen således lig afstanden fra trykbuens midte til væggens midte. Den resulterende excentricitet i midtersnittet fås som summen af denne excentricitet og bidraget e_init = h_ef / 450 fra imperfektioner og et eventuelt bidrag e_k fra krybningen udregnet efter formel (6.8) i EN 1996 - 1 - 1. Med denne resulterende excentricitet kan reduktionskapacitetsfaktoren Φ_m i væggens midte findes, og det kan afgøres om væggen kan overføre de givne laster.

Bæreevnen af en lodret belastet muret væg med samtidig vandret last beregnes normalt kun med hensyntagen til murværkets trykstyrke. Dette betyder, at når den lodrette last er lille i forhold til den vandrette, fås ingen eller næsten ingen bæreevne. Som følge heraf foretager programmet også en beregning af væggen, hvor væggens bøjningstrækstyrke ved bøjning om liggefugerne tages i regning. Denne beregning udføres efter den udvidede Navier-metode, og bæreevnen skal blot være tilstrækkelig enten efter den traditionelle EN 1996 - 1 - 1-beregning eller efter Navier-beregningen. Se nærmere i resultatrapporten under Generelle forudsætninger.

Parameteren e_init tager hensyn til konstruktionsimperfektioner

Der tages hensyn til e_init på følgende måde:

• EN 1996 - 1 - 1 - beregning: Excentricitetsintervallet indsnævres med værdien e_init i begge sider.
• Udvidet Navier beregning: Excentricitetsintervallet flyttes med værdien e_init til ugunst som funktion af vindretningen. Excentricitetsintervallet afskæres om nødvendigt så det ligger indenfor vægtykkelsen. Lastresultanten regnes at stå ugunstigt i intervallets trediedelspunkt svarende til en trekantet reaktionsfordeling.

I begge tilfælde benævnes det korrigerede excentricitetsinterval som det "regningsmæssige excentricitetsinterval"

Forskellen skyldes at:

• EN 1996 - 1 - 1 - beregningen er en plastisk model. Her antages, at revnefordelingen giver mulighed for omlejring af spændinger og at tryklinien i top og bund indstiller sig gunstigt mht excentriciteten i midten.
• Den udvidede Navier beregning er en elastisk model. Her antages, at tværsnittet er urevnet og i top og bund en lastresultant til ugunst ift. vindlasten. Et "flyttet" excentricitetsinterval er således til ugunst ift et indsnævret.

Bemærk: Bæreevnen bør ikke baseres på bøjningstrækspændinger såfremt der er risiko for et progressivt brud.

Bemærk: Såfremt forholdet mellem E_0k og f_k er mindre end 500 kan beregningen ikke gennemføres. Dette skyldes, at formeludtrykket i EN 1996-1-1 er rent empirisk og optimeret til E_0k/f_k = 1000. For lave værdier af dette forhold stiger bæreevnen markant såfremt f_k reduceres og alle andre parametre fastholdes. Dette virker ikke korrekt, hvorfor beregningen afbrydes.

I praksis er der 2 metoder til at løse dette problem:

• Beregningen foretages efter Ritter metoden (her kan excentriciteten eventuelt også være være til gunst i toppen bestemt ud fra metoderne angivet under Phi - metoden (altså fx stift dæk, fuld vederlag, etc giver excentricitet til gunst))
• Den fundne trykstyrke reduceres således, at forholdet mellem E_0k /f_k > 500 og beregningen kan gennemføres. Det antages, at en reduktion af f_k er konservativ

Biaksial bøjning: I EC6 er der ingen regler for biaksial bøjning (eller toakset bøjning). Såfremt en muret væg undergår en sådan påvirkning foreslås, at der tages udgangspunkt i reglerne i EC2, afsnit 5.8.9, hvor formel (5.39) angiver en simpel potensformel til undersøgelse af sådanne tilfælde.

 

Understøtningsforhold

En væg regnes altid understøttet i top og bund, og antallet af understøtninger er derfor mindst 2. En væg kan også være afstivet (understøttet) langs den ene eller langs begge dens lodrette kanter.

En vægs understøtningsforhold i top og bund karakteriseres ved en faktor ρ₂ som i EN 1996 - 1 - 1 enten tillægges værdien 0,75 eller 1,0. Da der i dette programmodul tages hensyn til understøtningsforholdene ved fastlæggelsen af væggens excentricitetsintervaller, sættes værdien af ρ₂ altid lig 1,0.

En væg kan regnes understøttet af en tværvæg langs en lodret kant hvis væggene er muret i forbandt eller samlingen er sikret af stående fortanding og bindere, og tværvæggens længde er mindst 1/5 af væghøjden h, og tværvæggens tykkelse er mindst 0,3 gange tykkelsen t af den afstivede væg.

Hvis tværvæggen indeholder huller på hver side af væggen skal den vandrette afstand mellem hullerne være større end

• (1/5) × (h₁ + h₂) / 2,

hvor h₁ og h₂ er højden af hullerne. Desuden skal tværvæggen fortsætte en strækning på mindst 1/5 af væghøjden forbi hver åbning som vist på figur 1.

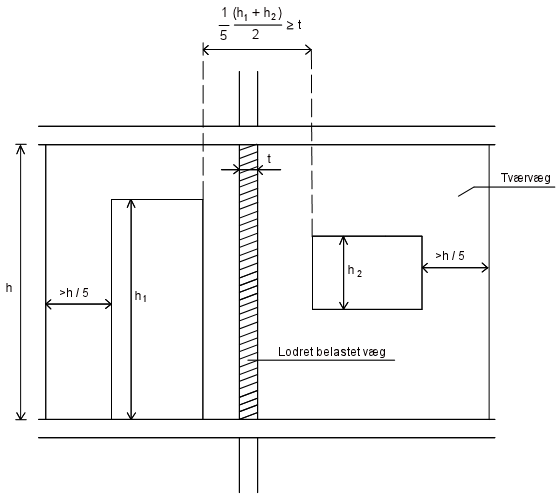
Figur 1. Minimum længde af tværvæg med åbninger.

 

Densitet

Værdien overføres automatisk fra fanebladet Murværk, men kan overskrives for den aktuelle komponent.

I flere moduler bestemmes væggens egenlast pr. m² vægflade som densiteten gange vægtykkelsen. Hvis et evt. pudslag ønskes medregnet til egenlasten, må densiteten sættes tilsvarende højere, idet vægtykkelsen af hensyn til bæreevnen ikke må angives med en for stor værdi.

  

Elasticitetsmodul E₂ og E₁

E₂ er den bærende vægs elasticitetsmodul.

E₁ er den eventuelle formurs elasticitetsmodul.

Hvis der ikke er nogen formur, er værdien af E₁ uden betydning.

Ved små tværsnit (mindre end 0,1 m², men dog større end 0,04 m²) bliver styrkerne reduceret iht EN 1996 - 1 - 1.

Værdierne overføres automatisk fra fanebladet Murværk (E_0k), men kan overskrives for den aktuelle komponent.

    

Excentricitetsintervalgrænser. Overordnet

Excentricitetsintervallernes grænser angives ved deres afstande fra væggens midte regnet positivt mod højre. Brugeren vælger selv hvilken af væggens sider der er højre, men valget gælder også for tværlasten, som regnes positiv mod venstre. Afstandene kan naturligvis være negative.

Excentricitetsintervallet angiver det område, hvor det er muligt at overføre reaktionerne/spændingerne i top og bund incl. reduktion fra "e_init" og "e_k".

Vederlagsintervallet angiver det interval, hvor konstruktionerne geometrisk "mødes". I mange tilfælde er excentricitetsintervallet det ½ af vederlagsintervallet, da væggen står og "vipper" som følge af vindlasten/bøjning/søjlevirkning.

For at kunne bestemme værdien af kapacitetsreduktionsfaktoren Φ i de 3 snit som EN 1996 - 1 - 1 kræver undersøgt, er det nødvendigt at bestemme den lodrette lasts excentricitet og excentricitetsbidraget fra den vandrette tværlast i de 3 snit.

(EN 1996 - 1 - 1 giver i anneks C en metode til bestemmelse af den lodrette lasts excentricitet i toppen og bunden af en væg baseret på en elastisk model af den betragtede væg og de tilstødende vægge og dæk. Denne fremgangsmåde er meget følsom overfor de stivhedsantagelser, der benyttes og i mange tilfælde er resultatet uforeneligt med, at der ikke kan regnes med trækspændinger i væggen. Som følge heraf er der i annekset også angivet en metode til bestemmelse af excentriciteterne baseret på en antagelse om, at spændingerne i væggen kan omlejres som følge af revnedannelse således, at der ikke optræder trækspændinger. Hvorledes disse metoder kan gøres operationelle fremgår ikke klart. Dette anneks C anvendes ikke i Danmark)

Hvorledes disse metoder kan gøres operationelle fremgår ikke klart. Anneks C anvendes ikke i Danmark iht. beslutning i normudvalget.

I programmodulet er valgt en anden fremgangsmåde, der er i overensstemmelse med EN 1996 – 1 – 1. Metoden går kort fortalt ud på at undersøge om der i væggen er plads til en trykbue svarende til den lodrette normalkraft og den vandrette last som væggen påvirkes af, således at betingelserne i EN 1996 - 1 - 1 i væggens top, bund og i et midtersnit er opfyldte. På figur 2 er problemstillingen illustreret.

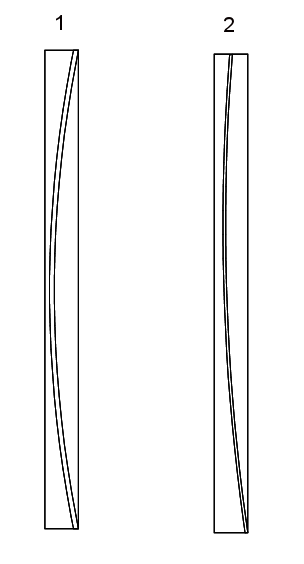
Figur 2. Placering af trykbue i væg.

I tilfælde 1 er excentriciteten til gunst i top og bund, fx svarende til stift dæk og stiv sokkel. Dette giver mulighed for optagelse af kraftig vindlast (lidt svarende til en indspændt søjle). I tilfælde 2 er bæreevnen lidt mindre da trykbuen i toppen ender midt i snittet svarende til, at lasten i toppen er fikseret fx af en smal toprem.

Rent inddatamæssigt betyder det, at i stedet for at angive excentriciteten af den lodrette last i væggens top og bund, som man alligevel ikke kan bestemme med nogen grad af sikkerhed, skal man angive et interval i væggens top og bund inden for hvilket trykbuens ender skal befinde sig. Disse intervaller kaldes excentricitetsintervaller.

Excentricitetsintervaller er relevante både for EN 1996 - 1 - 1 beregningen og den udvidede Navier beregning, hvor f_xk1 medregnes

Parameteren e_init

Parameteren e_init tager hensyn til konstruktionsimperfektioner

Der tages hensyn til e_init på følgende måde:

• EN 1996 - 1 - 1 - beregning: Excentricitetsintervallet indsnævres med værdien e_init i begge sider.
• Udvidet Navier beregning: Excentricitetsintervallet flyttes med værdien e_init til ugunst som funktion af vindretningen. Excentricitetsintervallet afskæres om nødvendigt så det ligger indenfor vægtykkelsen. Lastresultanten regnes at stå ugunstigt i intervallets trediedelspunkt svarende til en trekantet reaktionsfordeling.

I begge tilfælde benævnes det korrigerede excentricitetsinterval som det "regningsmæssige excentricitetsinterval"

Forskellen skyldes at:

• EN 1996 - 1 - 1 - beregningen er en plastisk model. Her antages, at revnefordelingen giver mulighed for omlejring af spændinger og at tryklinien i top og bund indstiller sig gunstigt mht excentriciteten i midten.
• Den udvidede Navier beregning er en elastisk model. Her antages, at tværsnittet er urevnet, og i top og bund er lastresultanten til ugunst ift. vindlasten. Et "flyttet" excentricitetsinterval er således til ugunst ift et indsnævret.

I nedenstående figur er vist det regningsmæssige excentricitetsinterval for EN 1996 - 1 - 1 - beregningen, hvor e_init er medtaget

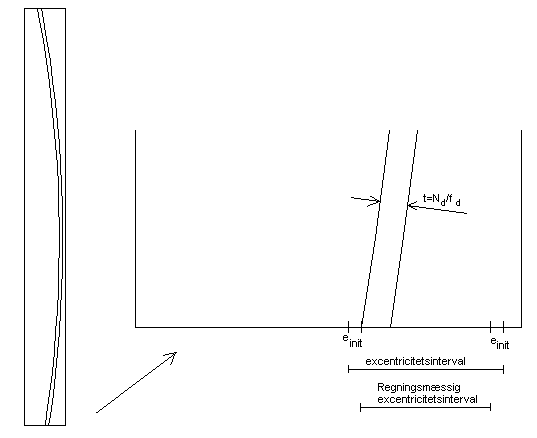
Figur 3. Placering af trykbue med hensyntagen til imperfektion e_init. EN 1996 - 1 - 1 - beregning.

Bæreevne

Med denne fremgangsmåde er betingelsen (6.4) i EN 1996 - 1 - 1 automatisk opfyldt i væggens top og bund. I midtersnittet er excentriciteten fra lasterne på væggen lig afstanden fra trykbuens midte til væggens midte. Den resulterende excentricitet i midtersnittet fås som summen af denne excentricitet og bidraget e_init = h_ef / 450 fra imperfektioner og et eventuelt bidrag e_k fra krybningen udregnet efter formel (6.8) i EN 1996 - 1 - 1. Med denne resulterende excentricitet kan reduktionskapacitetsfaktoren Φ_m i væggens midte findes og væggens bæreevne dermed bestemmes.

Bestemmelse af excentricitetsintervaller i praksis

Et excentricitetsinterval knyttet til toppen eller bunden af en væg angiver det område inden for hvilket den resulterende normalkraft i væggen skal befinde sig.

Excentricitetsintervallerne afhænger af væggens understøtningsforhold.

Betragtes en væg understøttet af et stift fundament vil væggen tendere mod at være understøttet enten på sit højre hjørne eller på sit venstre hjørne afhængig af retningen af tværlasten som vist på figur 4.

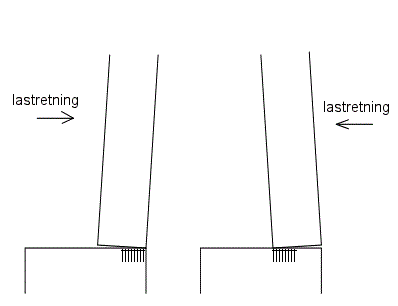
Figur 4. Væg på stift fundament. Excentricitet til gunst

(1) Uanset tværlastens retning vil reaktionen fra fundamentet flytte sig så, dens excentricitet virker til gunst for væggen. Excentricitetsintervallet kan i dette tilfælde sættes til den ½ vederlagsbredde til gunst.

Grunden til at excentricitetsintervallet ikke her sættes til den fulde bredde er, at trykkapaciteten i bunden (phi_bottom) herved vil blive overvurderet, da trykket kun bliver overført på den ydre del af væggen (og ikke hvor den "løfter sig"). I mange tilfælde for massive vægge uden søjlevirkning er phi_bottom dimensionsgivende. Lignende betragtninger kan foretages hvis væggen hviler på et betondæk eller belastes via et betondæk som må forventes at være væsentlig stivere end væggen.

(2) Såfremt dækket er slapt angives excentricitetsintervallet til den ½ vederlagsbredde til ugunst.

Er vederlaget smalt og udført af et blødere materiale end tegl/beton kan excentricitetsintervallet sættes lig vederlagsintervallet. Dette er illustreret nedenstående med en smal toprem af træ

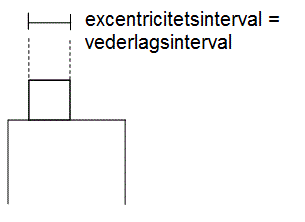
Figur 5. Excentricitetsinterval for væg belastet via en smal toprem.

Hvis topremmen ikke har et tværsnit som vist på figur 5, men nærmere er et bræt, skal excentricitets- og vederlagsintervallet formindskes jf ovenstående regler (altså reglerne angivet i (1) og (2)).

Det foreslås endvidere at sætte vederlagsintervallets bredde lig med 3 × h, dog naturligvis højst lig med b, altså vederlagsintervalbredde = minimum(b, 3h). Her er b remmens bredde og h dens højde. Se figur 6.

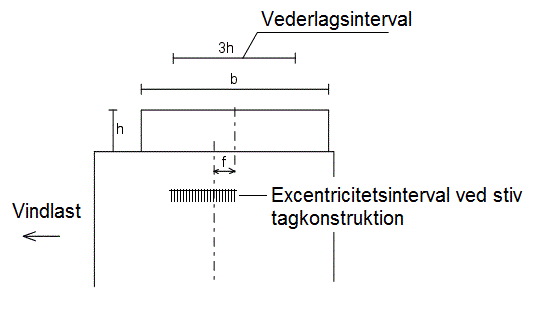
Figur 6. Angivelse af vederlags- og excentricitetsinterval ved brætformet toprem. Vederlagsintervallet regnes symmetrisk om topremmens midtlinie.

Som det ses, må den enkelte detalje granskes nøje ifm fastlæggelse af vederlagsinterval og excentricitetsinterval. Kun ved ren trykpåvirkning uden søjlevirkning og uden bøjning kan man regne med: tykkelse af væg = vederlagsinterval = excentritetsinterval. Dette vil i praksis være yderst sjældent.

Excentricitetsintervaller. Taleksempler

I væggens centerlinie er 0 – punktet indlagt. Excentricitetsintervallet til højre hhv. venstre for 0 – punktet angives som positiv og negativ.

Såfremt dækket/tagkonstruktionen er slap er excentricitetsintervallet den ½ bredde af vederlagsintervallet til ugunst.

Såfremt dækket vurderes som stift er excentricitetsintervallet den ½ bredde af vederlagsintervallet til gunst.

Se efterfølgende figur som eksempel

Dækket indlægges min. 70 mm på på væggen og reaktionen kan overføres på den ½ bredde (Her 35 mm).

Såfremt dækket vurderes som slapt bliver min - max værdierne hhv 49 og 84 mm.

Såfremt dækket vurderes som stift (ikke vist på figuren) bliver min - max værdierne hhv 14 og 49 mm

Ved bunden står væggen typisk på en stiv sokkel i fuld bredde. Her kan angives et excentricitetsinterval på -84 til 0 (som altså er den ½ vederlagsbredde og er til gunst).

En nærmere behandling af emnet findes i lærebogen, del 1 - afsnit 1 -3. Herunder en vurdering/beregning af om dæk/tagkonstruktion er stiv

Se:

www.mur-tag.dk

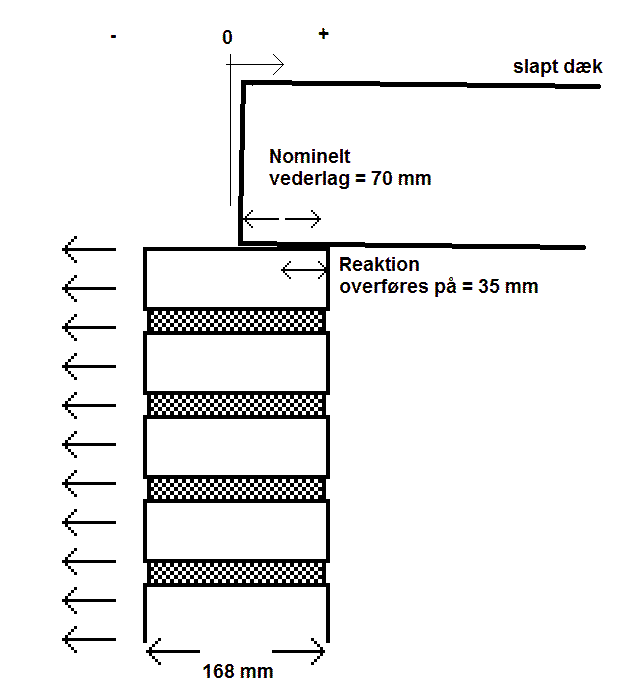
Figur 7. Slapt dæk med vederlag på en del af væggen. Taleksempel

I figur 8, skitse A, ses en typisk løsning ved dækkant for monolitiske vægkonstruktioner. I brudsituationen, skitse B (her illustreret med sug på væg) vil lasten fra væggen overføres i den yderste blok, mens dæklasten fortsat vil overføres gennem dækkets excentricitetsintervallet. Det samlede excentricitetsinterval kan findes ud fra de almindelige statiske ligevægtsligninger (skitse C)

Følgende parametre anvendes i eksemplet:

• N_væg = 10 kN
• N_dæk = 30 kN
• t₁ = 100 mm
• t₂ = 150 mm
• t = 400 mm

Forholdene ved yderste blok regnes for stive

Værdien for excentriciteten (e) (skitse D) bestemmes ud fra:

Stift dæk:

10(200 + e_stift - 100/4 = 30(200 - 3/4(150) - e_stift)

Hvoraf fås: e_stift = 22 mm

Slapt dæk (ikke vist på figuren):

10(200 + e_slapt - 100/4 = 30(200 - 1/4(150) - e_slapt)

Hvoraf fås: e_slapt = 78 mm

Topexcentriciteten indlægges således, at den faktiske excentricitet svarer til de fundne værdier. Fx:

Stift dæk: Fra 0 til 44 mm

Slapt dæk: Fra 56 til 100 mm

Bemærk: Det skal naturligvis sikres, at styrken af den yderste blok er tilstrækkelig

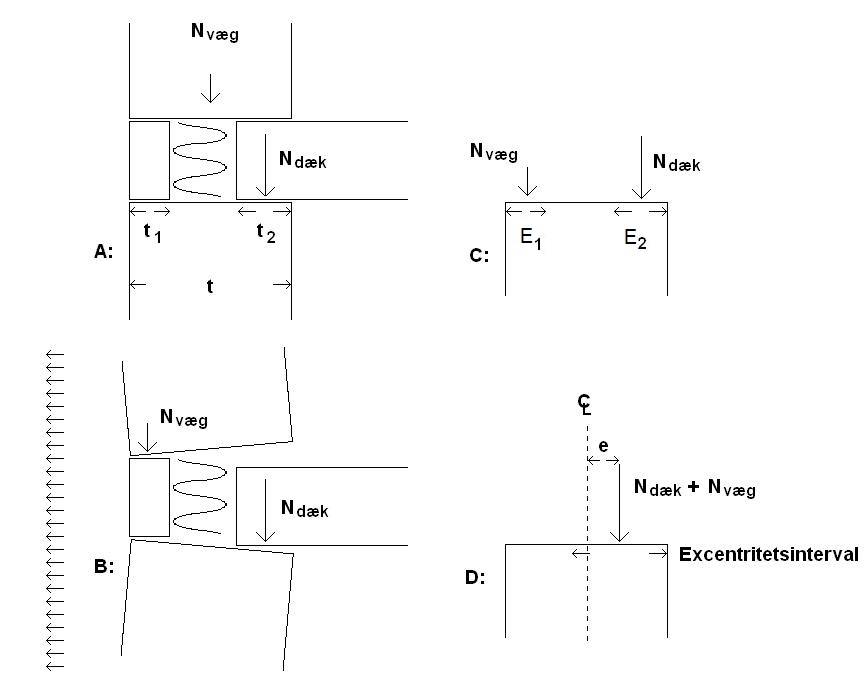
Figur 8. Dækkant. Stift dæk

 

Trykstyrke f_k

Ved små tværsnit (mindre end 0,1 m²) bliver styrkerne reduceret iht EN 1996 - 1 - 1.

Værdien overføres automatisk fra f_k på fanebladet Murværk, men kan overskrives for den aktuelle komponent.

 

Bøjningstrækstyrke f_xk1

Bemærk: Bæreevnen bør ikke baseres på bøjningstrækspændinger såfremt der er risiko for et progressivt brud.

Værdien overføres automatisk fra f_xk1 på fanebladet Murværk, men kan overskrives for den aktuelle komponent.

Ved små tværsnit (mindre end 0,1 m²) bliver styrkerne reduceret iht EN 1996 - 1 - 1.

   

Væggens geometri

Programmodulet "Lodret belastet muret væg efter EN 1996 - 1 - 1" kan beregne en bærende væg som enten kan være en enkelt væg eller en af vangerne i en hul mur.

Væggen skal mindst være fastholdt i vandret retning langs en vandret linie i toppen og i bunden. Væggen kan være afstivet langs den ene eller langs begge dens lodrette kanter.

Det sikres, at tykkelsen overholder eventuelle minimumskrav angivet i det nationale anneks N.A. (ikke aktuelt for DK)

 

Lodret last på væg

Den samlede lodrette last på væggen divideret med væggens effektive længde, dvs væggens samlede længde minus længden af mindre vinduesåbninger etc. Den lodrette lastintensitet uden hensyn til åbninger kan normalt fås fra modulet Lastberegning. Denne lastintensitet skal multipliceres med væggens samlede længde og divideres med væggens effektive længde.

Egenvægten skal ikke medtages i den lodrette last, da denne medtages via densiteten og tykkelsen

En lodret punktlast kan fordeles under 1:2.

Er væggen fx 2,8 m høj kan der for en punktlast øverst på den centrale del af vægfeltet (dvs min. 1,4 m / 2 = 0,7 m vandret fra den lodrette kant) regnes med en vandret udstrækning af vægfeltet på: 2 x 1,4 m/2 = 1,4 m.

Er den koncentrerede last beliggende på kanten kan regnes med en vandret udstrækning af vægfeltet på: 1 x 1,4 m/2 = 0,7 m.

I begge tilfælde skal tages hensyn til spaltekræfter, mulighed for vandret modhold i konstruktionen, etc. Disse forhold kan være kritiske.

Bemærk: I nogle tilfælde kan bæreevnen være tilstrækkelig med en kraftig lodret last, hvorimod bæreevnen for den samme konstruktion kan være utilstrækkelig, såfremt den lodrette last er ringe. Det kan virke underligt, at såfremt lasten er 500 kN/m kan væggen holde, hvorimod den ikke kan holde såfremt den lodrette last reduceres til 5,0 kN/m. Dette skyldes, at bæreevnen for ringe lodret last (i kombination med vindlast) skal etableres vha bøjningstrækstyrkerne som kan være små ift. trykstyrken samt at modulet ikke tager hensyn til eventuelle lodrette understøtninger.

Når den lodrette last er ringe er der sjældent søjlevirkning i normalt forekomne vægge og bæreevnen bør alene undersøges ud fra brudlinieteorien vha modulet tværbelastede vægge. Såfremt der er en kraftig lodret på væggen og væggen ønskes undersøgt som et hovedsageligt lodret belastet vægfelt skal vindlasten reguleres og den ækvivalente tværlast anvendes (denne er angivet sidst i udskriften i modulet tværbelastede vægge)

 

Tværlast (vind)

Tværlasten er næsten altid vindlast, som dels virker direkte på væggen, dels i nogle tilfælde overføres til eller fra væggen via jævnt fordelte bindere. Tværlasten forudsættes ensformigt fordelt over hele væggens areal. Den regnes positiv mod venstre (mens excentricitetsintervalgrænserne regnes positive mod højre).

Såfremt kubikrodsformlen anvendes og formuren regnes at stabilisere bagmuren, skal den totale vindlast regnes at påvirke bagmuren

 

Tykkelse af formur

Formuren kan, via kubikrodsformlen, medregnes til at stabilisere bagmuren. Effekten indregnes ved bestemmelse af den belastede vanges effektive tykkelse t_ef.

Såfremt kubikrodsformlen anvendes og formuren dermed regnes at stabilisere bagmuren, skal den totale vindlast regnes at påvirke bagmuren

Det sikres, at tykkelsen overholder eventuelle minimumskrav angivet i det nationale anneks N.A. (ikke aktuelt for DK)

---